Mathematikela steht für: Mathematik mit elektronischen Arbeitsblättern

Wie möchtest du arbeiten?

Im Detektivmodus 🕵 kannst du Aufgaben ergründen 🔍 und es gibt auch Lösungstipps 💡.
Im Modus Hausaufgaben erhältst du am Ende einen Lösungssatz.
Im Prüfungsmodus ⏱ gibt es eine Zeitbegrenzung und du erhältst deine Punktzahl erst am Ende.

Aufträge

• Teil 1: Vom Rechteck ▭ zum Dreieck 🔺

  Wiederholung: Figuren haben eine Flächengröße

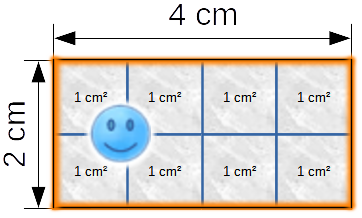
  Der Innenteil einer Fläche hat eine Größe und diese wird häufig in Quatratzentimeter (cm²) angegeben (bei kleinen Flächen). Smiley zeigt dir hier, wie sich Flächen ändern, wenn mehrere Quadratzentimeter ohne Abstand nebeneinandergelegt werden:
  

  Wie sieht es hier aus?
  
  

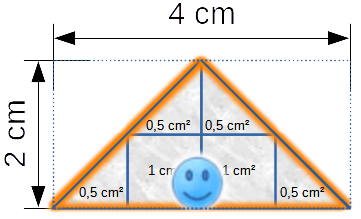
  Das ursprüngliche Rechteck wurde zum Dreieck verkleinert. Wie groß ist jetzt der Flächeninhalt?
  
  

  Ideen zu Dreiecken 🔺

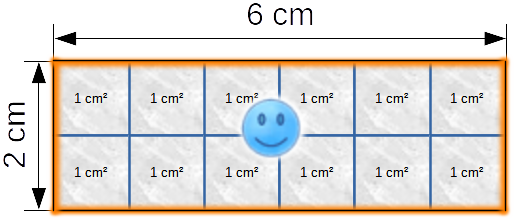
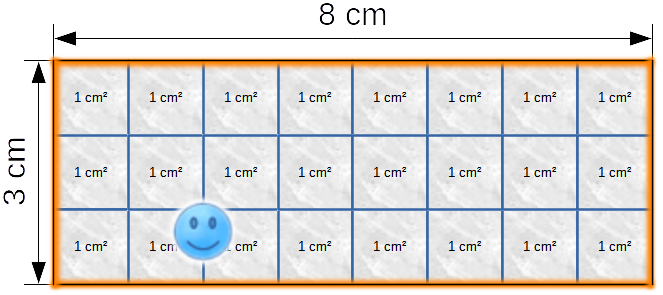
  Wie groß ist jetzt der Flächeninhalt dieses Rechtecks?
  
  

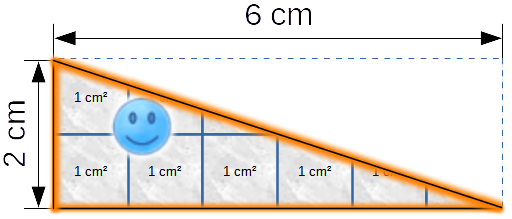
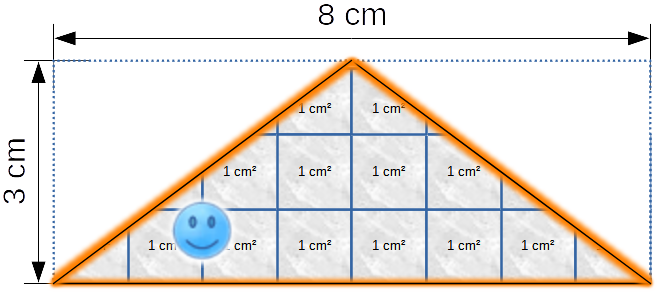
  Das ursprüngliche Rechteck wurde zum Dreieck verkleinert. Wie groß ist jetzt sein Flächeninhalt?
  
  

  
  

  
  

  Flächeninhalt von Dreiecken, ganz allgemein

  Schneidest du ein Dreieck aus Papier aus, so hat es eine bestimmten Flächeninhalt. Jetzt ist es so, dass jedes Dreieck auf bestimmte Art und Weise zu einem flächengleichen Rechteck umgelegt werde kann. Du brauchst dazu nur zwei Schnitte zu machen und erhältst mit etwas Geschick ein Rechteck mit gleicher Flächengröße.
  Schau dir die Anmiation mal genau an:
  Sie läuft von alleine, du kannst aber mit der Maus bzw. durch Wischen blättern

  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 

  Der Flächeninhalt eines Dreiecks 🔺

  Man kann immer ein Dreieck 🔺 durch 2 Schnitte so umformen, dass ein Rechteck ▭️ mit gleichem Flächeninhalt entsteht. Dieses Rechteck ▭️ hat immer noch die gleiche Höhe wie das Dreieck 🔺 aber nur die Hälfte der Länge der Grundseite, hier also 0,5·c oder auch ½·c
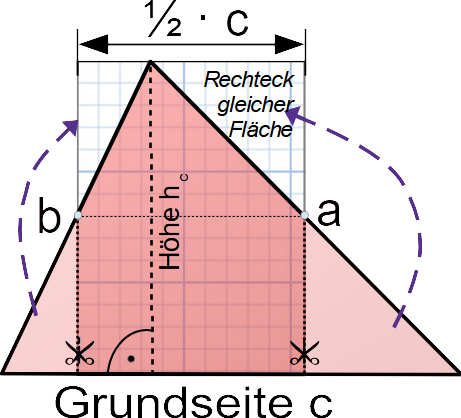
  Der Flächeninhalt eines Dreiecks ist also die halbe Grundseite mal zugehörige Höhe. Als Formel: A_🔺 = ½ · c · h_c
  Und so geht's auch: A_🔺 = 0,5 · c · h_c

  Dreiecke

  
  

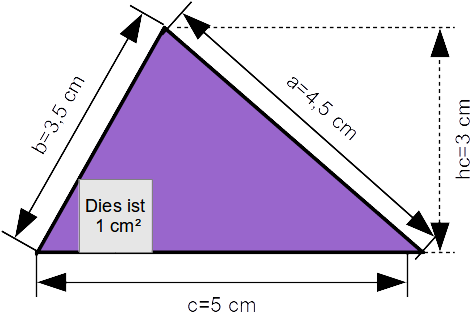
  Der Umfang eines Dreiecks u = a + b + c

  Beim Umfang werden alle drei Seitenlängen des Dreiecks addiert:
  

  Die Dreiecksformeln funktionieren auch hier:

  
  

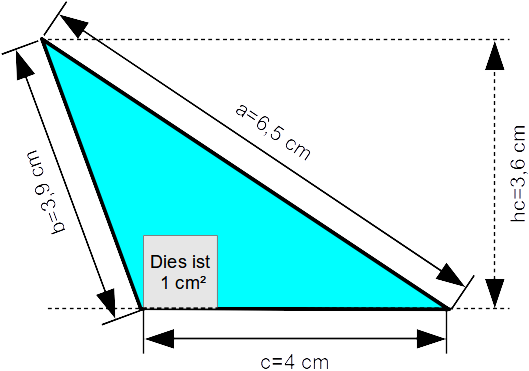
  Flächeninhalt von Dreiecken bei denen die Höhe über die Seite a gegeben ist.

  
  

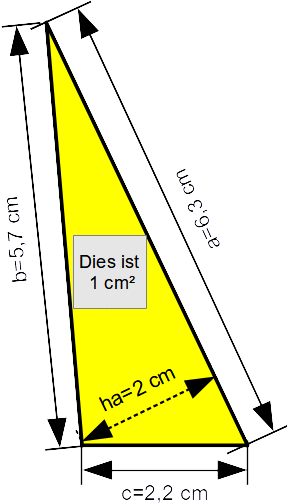
  Aufgabe zu Dreiecken, jetzt mal ohne Bild

  Gegeben: Grundseite c = 10cm und h_c= 11cm
  Gesucht: Flächeninhalt des Dreiecks

  Noch eine solche Aufgabe zu Dreiecken

  Gegeben: Seite a = 12cm und h_a= 4cm
  Gesucht: Flächeninhalt des Dreiecks

  Textaufgabe zu Dreiecken

  Ein dreieckiges rahmenloses Fenster wird an einer Seite eines Hauses eingebaut. Die waagerechte Grundseite beträgt 3 m und die Höhe ist 1,8 m
  Gegeben: c = 3 m und h_c= 1,8 m
  Gesucht: Flächeninhalt A des dreieckigen Fensters

  Das dreieckige Fenster braucht zur Befestigung Holzleisten, die insgesamt so lang sind wir der Umfang des Dreiecksfensters. Berechne zunächst den Umfang des Dreieckfensters. Gegeben: Seite c = 3 m und a = b = 2,01 m
  Gesucht: Umfang des Dreiecks

• Teil 2: Parallelogramme sind besondere 4Ecke

  Verschiedene Figuren und ein Parallelogramm

  Smiley zeigt dir hier seine Wohnung, die nun mehr als 1 cm² Wohnfläche hat. Er hat für den Anbau rechts einen Quadratzentimeter in der Mitte geteilt und hat nun 0,5 cm² mehr Wohnraum.
  

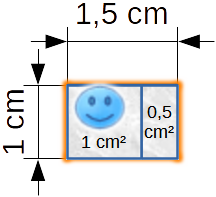
  Smiley hat für den Anbau rechts ein Dreieck angebaut (ein Quadrat, das diagonalt geteilt wurde) und hat nun 0,5 cm² mehr Wohnraum.

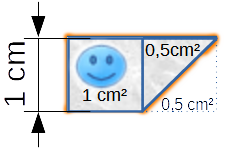
  Wie sieht es hier aus?
  
  

  
  

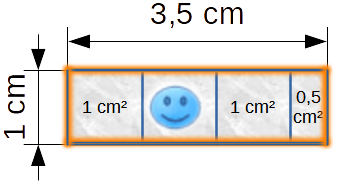
  Und jetzt wurden Dreiecke links und rechts hinzugefügt
  Damit sind gegenüberliegende Seiten: 1. gleich lang und
  2. verlaufen sie parallel zueinander.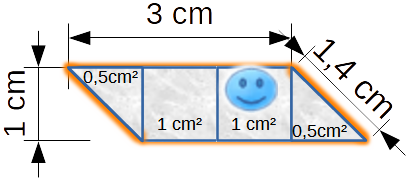
  

  Und jetzt ein etwas größeres Parallelogramm:
  
  

  Bisher hast du nur einfache Parallelogramme kennengelernt, der Flächeninhalt war noch recht einfach durch Abzählen zu ermitteln. Aber Parallelogramme können beliebig Schrägen haben und damit umzugehen, das kommt als Nächstes.

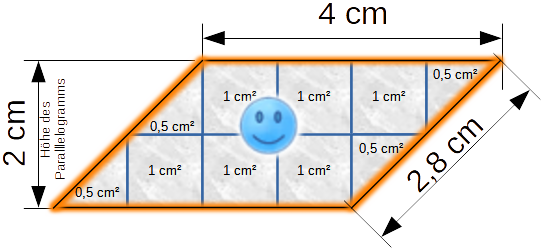
  Flächeninhalt von Parallelogrammen ▱, ganz allgemein

  Bei jedem Parallelogramm kannst du mittig eine Parallele einzeichnen, die die Figur in 2 Hälften zerteilt. Wenn du nun mit der Schere die Dreiecksüberstände abschneidest, dann können diese neu angelegt werden. Es entsteht ein Rechteck mit gleichem Flächeninhalt.
  Schau dir die Anmiation mal genau an:
  Sie läuft von alleine, du kannst aber mit der Maus bzw. durch Wischen blättern

  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 
  • 

  Der Flächeninhalt eines Parallelogramms ▱

  Man kann immer ein Parallelogramm ▱ durch 1 bzw. 2 Schnitte so umformen, dass ein Rechteck ▭️ mit gleichem Flächeninhalt entsteht. Dieses Rechteck ▭️ hat immer noch die gleiche Höhe wie das Parallelogramm ▱ und die Länge der Grundseite bleibt auch gleich.
  

  
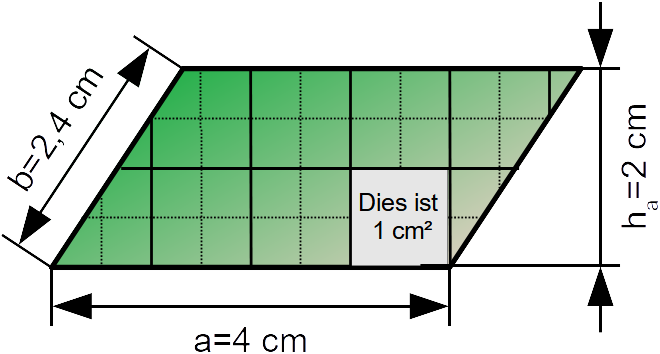
  Der Flächeninhalt eines Parallelogramms ▱ ist also die Grundseite a mal zugehörige Höhe. Als Formel:
  A_▱ = a · h_a Der Flächeninhalt eines Parallelogramms ▱ kann auch über die Seite b und die zugehörige Höhe erfolgen. Als Formel:
  A_▱ = b · h_b

  Der Umfang eines Parallelogramms ▱

  Parallelogramme ▱, Flächeninhalt auf zwei Arten berechnen

  Dieses Parallelogramm wurde aus Papier ausgeschnitten.
  
  

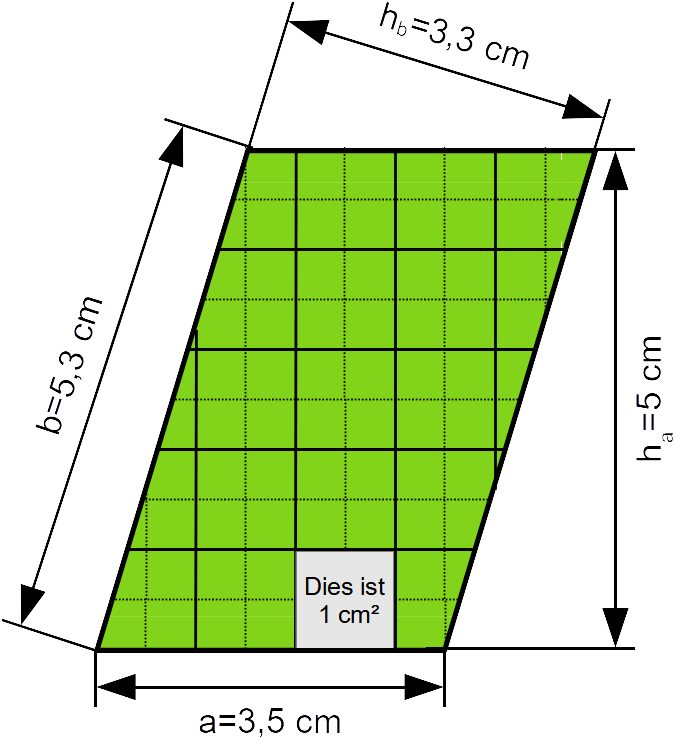
  Nun auf die zweite Art und Weise

  Wenn alles korrekt läuft, muss (fast) das gleiche Ergebnis herauskommen.

  Vergleiche mit dem Ergebnis weiter oben, es ist (fast) identisch. Was du hier siehst sind ganz übliche Ungenauigkeiten, denn man kann die Seitenlängen nicht ganz genau angeben.

  Wann genau wird ein Parallelogramm zur Raute ?

  Dieses Parallelogramm wurde aus Pappe ausgeschnitten.
  
  

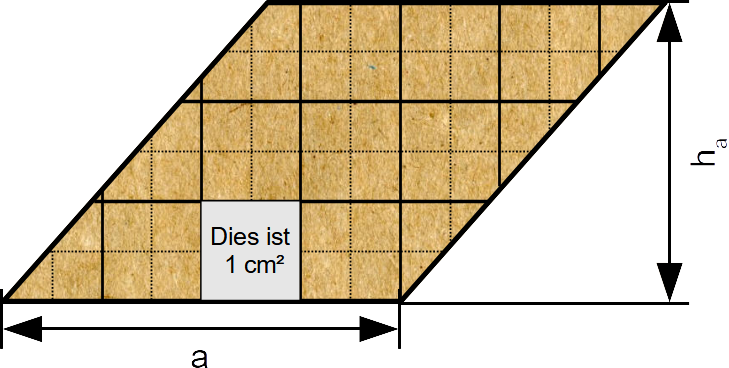
  Nun ist der Umfang gesucht

  Häufig werden Rauten so dargestellt

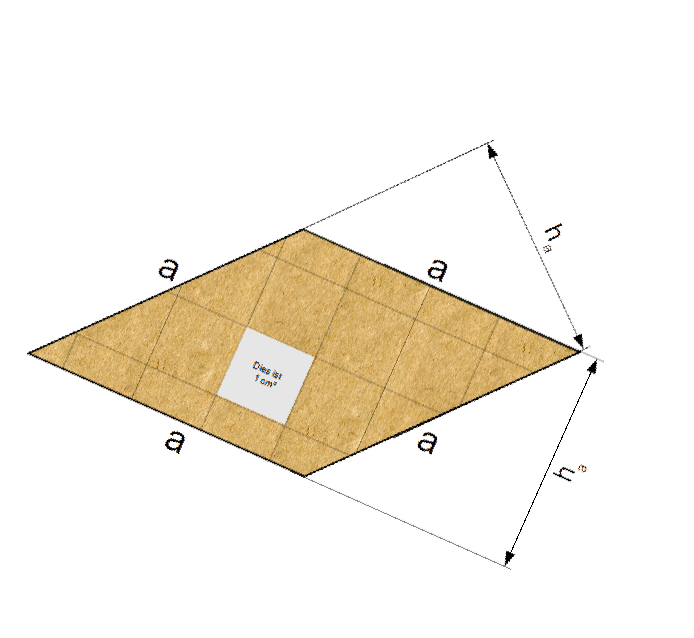  Da bei Rauten die 4 Seiten gleich lang vereinfacht sich der Umfang zu:
  u = 4 · a

  Du hast nun diesen Teil bearbeitet. Hervorragend!
  Atme mal durch.
  Diese Übungen mit Flächeninhalten waren ein Anfang, aber hoffentlich ein Guter 😀. Es ist wichtig, dass du nun Aufgaben aus dem Buch und auf eigenem Papier bearbeitest, um ein eigenes Erlebnis 🧐 davon zu bekommen.