Mathematikela steht für: Mathematik mit elektronischen Arbeitsblättern

Wie möchtest du arbeiten?

Im Detektivmodus 🕵 kannst du Aufgaben ergründen 🔍 und es gibt auch Lösungstipps 💡.
Im Modus Hausaufgaben erhältst du am Ende einen Lösungssatz.
Im Prüfungsmodus ⏱ gibt es eine Zeitbegrenzung und du erhältst deine Punktzahl erst am Ende.

Aufträge

• Teil 1: Die Hälfte, ein Viertel oder ein Drittel einer Menge

  Einstieg

  
  

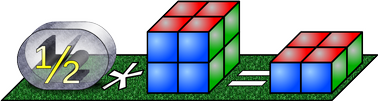
  Oft wollen wir wissen, wie viel die Hälfte einer Menge ist. Ist die ursprüngliche Menge 8, dann schreiben wir: ½ * 8 (sprich: "ein halb mal acht")

  Gesucht ist jetzt jeweils ein Viertel der Menge

  
  

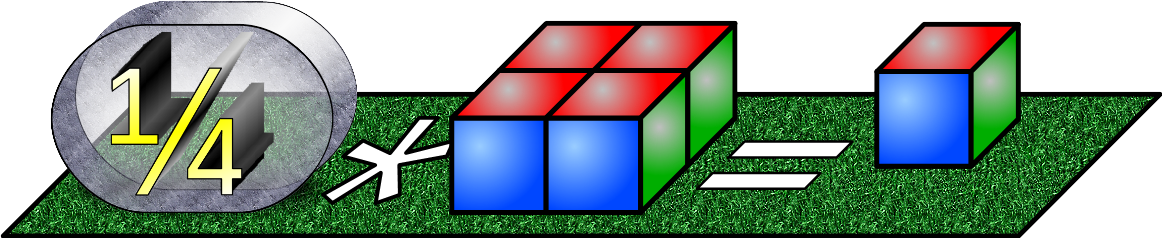
  Oft wollen wir wissen, wie viel ein Viertel einer Menge ist. Ist die ursprüngliche Menge 4, dann schreiben wir: ¼ * 4 (sprich: "ein Viertel mal vier oder: ein Viertel von vier")

  Drei Viertel einer Menge?

  
  

  Oft wollen wir wissen, wie viel drei Viertel einer Menge ist. Ist die ursprüngliche Menge 8, dann schreiben wir: ¾ * 8 (sprich: "drei Viertel mal vier oder: ¾ von 8")

  Drei Achtel einer Menge?

  
  

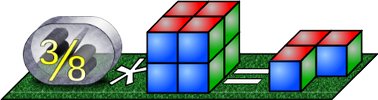
  Oft wollen wir wissen, wie viel drei Achtel einer Menge ist. Ist die ursprüngliche Menge 8, dann schreiben wir: ⅜ * 8 (sprich: "drei Achtel mal acht oder: ⅜ von 8")

  Zehntel einer Menge?

  
  

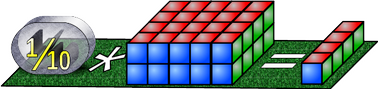
  Oft wollen wir wissen, wie viel ein Zehntel einer Menge ist. Ist die ursprüngliche Menge 40, dann schreiben wir: ⅒ * 40 (sprich: "ein Zehntel mal Vierzig oder: ⅒ von 40")

  Fünftel einer Menge?

  
  

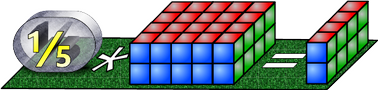
  Oft wollen wir wissen, wie viel ein Zehntel einer Menge ist. Ist die ursprüngliche Menge 40, dann schreiben wir: ⅕ * 40 (sprich: "ein Zwanzigstel mal Vierzig oder: ⅒ von 40")
  Rechentipp, es gilt ja: ⅕ = 2 * ⅒. Daher kann man rasch ein Zehntel der Menge bilden und dies verdoppeln.

  Ein Zwanzigstel einer Menge?

  
  

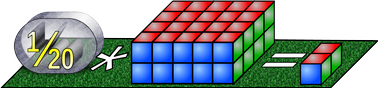
  Oft wollen wir wissen, wie viel ein Zehntel einer Menge ist. Ist die ursprüngliche Menge 40, dann schreiben wir: ¹⁄₂₀ * 40 (sprich: "ein Zwanzigstel mal Vierzig oder: ¹⁄₂₀ von 40")
  Rechentipp, es gilt ja: ¹⁄₂₀ = ½ * ⅒ und das heißt ¹⁄₂₀ ist die Hälfte von ⅒. Daher kann man rasch ein Zehntel der Menge bilden und dann nochmals halbieren.

  Ein Hundertstel einer Menge?

  
  

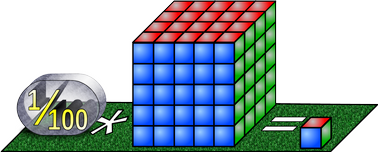
  Oft wollen wir wissen, wie viel ein Hundertstel einer Menge ist. Ist die ursprüngliche Menge 100, dann schreiben wir: ¹⁄₁₀₀ * 100 = 1 (sprich: "ein Hundertstel mal Hundert oder: ¹⁄₁₀₀ von 100")
  Rechentipp, es gilt ja: ¹⁄₁₀₀ = ⅒ * ⅒ und das heißt ¹⁄₁₀₀ bedeutet, die gegebene Menge zweimal durch 10 teilen.
• Teil 2: Prozente %

  0,01 = 1/100 = 1 Prozent

  
  

  Diese ganze Vorarbeit diente dazu, zu verstehen, wie wir in der Mathematik Teile eines Ganzen ausdrücken können. Bedeutend für unseren Alltag ist die Angabe in Prozenten. '1 Prozent' meint den Hundertsten Teil vom Ganzen und '50 Prozent' meint die Hälfte vom Ganzen. Um auch Prozent kürzer zu schreiben gibt es das Prozentzeichen und so sieht es aus: %
  Die Hälfte = 50 Prozent = 50 % = 0,5 = ½
  Notiere nun jeweils die fehlende Dezimalzahl:

  1/5 = 20 Prozent = 0,2

  'EinFünftel' einer Menge meint auch: Wie viel sind 20% davon. Das entspricht jeweils dem 0,2fachen einer gegebenen Menge. Denn: Man kann 1/5 erweitern auf einen Bruch mit dem Nenner Hundert erweitern:
  1/5 = 20/100 = 20 Prozent = 20%
  Und es gilt: 20% = 0,2.
  Notiere zunächst die jeweils fehlende Dezimalzahl:

  ½ = 50 %
  Aber: ⅓ ist nur ungefähr 33,3%

  ½ ist gleich 50%, ist klar. Aber wir müssen über ein Drittel reden. Streng genommen, lässt sich dieser Bruch nicht als Dezimalzahl schreiben, daher setzt man noch eine Kommastelle hinzu und dann ist (in diesem Fall) genau genug.
  Das Ungefährzeichen ist '≈', also gilt: ⅓ ≈ 0,333 = 33,3%. So machen wir es auch mit ⅔≈0,667=66,7% oder mit ⅙≈0,167=16,7%. Das üben wir nun, gib jeweils die Prozentzahl an, du musst auch das Zeichen % angeben.

  50% von irgendetwas ist ...

  Wir fangen ganz langsam an: 50% von einer Menge meint stets die Hälfte dieser Menge, also das 0,5fache dieser Menge.
  Frage: Wie viel sind 50% von 80 Liter? Es ist die Hälfte, also 40 Liter
  Kürzere Schreibweise: 50% von 30 m sind 15 m
  Und ganz kurz: 50% von 12 € = 6 € und wenn wir die Einheit weglassen, dann: 50% von 25 = 12,5. Und jetzt bist du dran:

  ¼ = 0,25 = 25 Prozent = 25%

  'Einviertel' einer Menge sind die Hälfte von der Hälfte einer gegebenen Menge. In diesem Fall sind das auch das 0,25fache der Menge bzw. 25% von dieser Menge. 25% von 16 = 4. Jetzt du:

  3/4 = 0,75 = 75 Prozent = 75%

  'Dreiviertel' einer Menge sind 75 % und entspricht dem 0,75fachen der Menge. Denn: Man kann 3/4 erweitern auf einen Bruch mit Hundertstel: 3/4 = 75/100 und das sind 75 %. Wenn die Grundmenge 20 Liter Wasser sind, dann sind 75% davon Dreiviertel dieser Menge.
  Ein Rechentipp: Suche zuerst ein Viertel der Menge und multipliziere mit 3. 75% von 20 Liter sind also 15 Liter. Ok?
• Teil 3: Jetzt geht es richtig los, werde zum Rechenmeister in der Prozentrechnung.

  0,1 = 1/10 = 10 Prozent = 10%

  10% meint immer den Zehnten Teil einer Menge.
  20% meint immer zen Fünften Teil einer Menge (Tipp, es ist stets das Doppelte von 10%)

  0,01 = 1/100 = 1 Prozent = 1%

  1% meint immer den Hundersten Teil einer Menge. Tipp: durch 10 dividieren und nochmals durch 10 dividieren.
  Und 2% ist ja das Doppelte von 1%.

  0,1 = 10% und 0,2 = 20%, ...

  20% meint das Doppelte von 10%
  30% meint das Dreifache von 10% usw. Gutes Gelingen.

  0,05 = 5 Prozent = 5% und 0,15 = 15%

  5% ist genau die Hälfte von 10%.
  15% sind 10% und 5% zusammengenommen.
  Volle Konzentration, es geht los!

  0,15 = 15 Prozent = 15% und 0,35 = 35%

  15% sind 10% plus 5% zusammen.
  35% sind 30% und dazu noch 5%. Das ist der wichtige Trick dazu!

  0,12 = 12% = 10% + 2%

  12% sind 10% + 2%. Beispiel: Wie viel sind 12% von 20? Also 10% von 20 sind 2 und 2% von 20 sind 0,4.
  Also sind 12% von 20 somit 2,4.
  9% meint 10% minus 1%. Beispiel: 9% von 30 sind?
  Also 10% sind 3 und 1% sind 0,3, und 3-0,3=2,7.
  9% von 30 sind also 2,7. Gutes Gelingen!

  Du bist hier und hast alles bearbeitet?
  Dann bist du jetzt fertig. Lehn dich zurück, super gemacht!