Mathematikela steht für: Mathematik mit elektronischen Arbeitsblättern

Wie möchtest du arbeiten?

Im Detektivmodus 🕵 kannst du Aufgaben ergründen 🔍 und es gibt auch Lösungstipps 💡.
Im Modus Hausaufgaben erhältst du am Ende einen Lösungssatz.
Im Prüfungsmodus ⏱ gibt es eine Zeitbegrenzung und du erhältst deine Punktzahl erst am Ende.

Aufträge

• Teil 1: Zeit bei Zinsen berücksichtigen

  💶 Zinsen innerhalb eines Jahres 💶

  🏦 Tage und Monate im Bankwesen 🏦

  Schau dir als Einstieg dieses Video über die Zinsrechnung an.

  Die vier Jahreszeiten lauten:
  Frühling: 🌼, Sommer: 🏖, Herbst: 🍁 und Winter: ❄.
  Die Jahreszeiten unterteilen gewissermaßen ein Jahr 4 gleich große Abschnitte.

  % Wiederholung Prozent %

  Wiederholung: Was bedeutet der Zinssatz 2 Prozent?
  
  Da das Wort Prozent übersetzt 'pro Hundert' heißt, kann 2% auch als Bruch ²⁄₁₀₀ geschrieben werden und das ist dann die auch die Kommazahl 0,02.
  Rechne nun verschiedene Zinssätze in Kommazahlen um:

  Wiederholung Zinsrechnung: Im Bankwesen, wo es ja stets um Geld geht, spricht man vom Zinssatz, abgekürzt: p%. Spart man sein Geld bei der Bank, dann gibt es dafür eine Geldbelohnung zum Jahresende Zinsen. Diese Zinsen hängen davon ab, wie viel Geld genauer: Kapital man angelegt hat und zu welchem Zinssatz.
  ZINSEN = KAPITAL · ZINSSATZ
  Zinsen = K · p%

  • Auf Wunsch kann hier eine Tabelle ausgeklappt werden, die die Ähnlickeit der Prozentrechnung und der Zinsrechnung (mit Jahreszinsen) zeigt:

    Prozentrechnung	Zinsrechnung (im Sinne von Jahreszinsen)
    Grundwert, kurz G Der Grundwert ist das Ganze, von dem man zunächst ausgeht.	Kapital, kurz: K So viel Geld hat man zu Beginn des Jahres zur Bank gebracht.
    Prozentsatz, kurz: p%	Zinssatz, auch abgekürzt: p%
    ProzentWert	Zinsen, kurz Z
    Formel der Prozentrechnung: ProzentWert = Grundwert mal Prozentsatz	Formel für die Jahreszinsen: Zinsen = Kapital mal Zinssatz
    rechte Seite in Formelzeichen: ProzentWert = G · p%	rechte Seite in Formelzeichen: Zinsen = K · p%

  Wie viel Jahreszinsen bringen 200 € bei der Bank bei 2 % Zinssatz?

  Der Zinssatz p%=2 % meint: Wir suchen das 0,02fache (😉 2 % =   ² ₁₀₀= 0,02 !) des angelegten Geldes. Pro 100 € auf der Bank sind das 2 € Zinsen.

  Das Üben wir jetzt, gib jeweils die Zinsen an: Noch ein Rechentipp: 2% ist das Doppelte von 1%, berechne also erst 1% und verdopple dann.

  💶 Zinsen bei der 🏦 für ein halbes Jahr

  Angelegtes Geld bei der 🏦 mit einer ⏳ Zeitspanne von 6 Monaten = 6 📅 = ½ Jahr

  Beträgt die angelegte Zeit bei der Bank nur ein halbes Jahr, dann gibt es auch nur die Hälfte der Jahreszinsen.

  💶 Zinsen, wenn 💶 bei der 🏦 nur für ein Vierteljahr angelegt ist

  Angelegtes Geld bei der 🏦 mit ⏳ Zeitspanne: 3 Monate = 3 📅 = ¼ Jahr

  Beträgt die angelegte Zeit bei der Bank nur ein Vierteljahr, dann gibt es entspechend weniger Zinsen.

  💶 Zinsen bei der 🏦, angelegte Zeit ⏳: 1 Monat

  Alles gleiche ⏳ Zeitspannen: 1 📅 = 1 Monat = ¹⁄₁₂ Jahr

  Beträgt die angelegte Zeit bei der Bank nur einen Monat, dann gibt es auch nur ein Zwölftel (als Bruch: ¹⁄₁₂) der Jahreszinsen.

  Rechentipp: Ein Zwölftel kannst du berechnen, indem du erst durch 3 teilst und dann nochmals durch 4 teilst.
  Denn: ¹⁄₁₂= ⅓ · ¼.
  Beispiel: 30€ · ¹⁄₁₂ = 30€ · ⅓ · ¼ = 10€ · ¼ = 2,50€.

  💶 Zinsen bei der 🏦, angelegte Zeit ⏳: 40 Tage

  40 Tage = ⁴⁰⁄₃₆₀Jahr = ⅑ Jahr

  Manchmal ist es so, dass man ein größeren Geldbetrag nur für mehrere Tage bei der Bank belässt, bis ein größerer Kauf (🚗, 🏍, 🏡) ansteht. Das könnten zum Beispiel 40 Tage sein, und unser Bankjahr hat ja 360 Tage. Also: ⁴⁰⁄₃₆₀ = ⁴⁄₃₆ = ²⁄₁₈ = ⅑.
  Das bedeutet: Da 40 Tage nur ein Neuntel vom Jahr (kurz: ⅑ a) sind, gibt es auch nur ⅑ der Jahreszinsen.

  💶 bei der 🏦 und Zinsen für ⏳ 20 Tage

  20 Tage = ²⁰⁄₃₆₀Jahr = ²⁄₃₆Jahr = ¹⁄₁₈ Jahr

  Da 20 Tage nur ein Achtzehntel vom Jahr ist (kurz: ¹⁄₁₈ a), gibt es auch nur ¹⁄₁₈ der Jahreszinsen.

  💶 bei der 🏦 und Zinsen für ⏳ 72 Tage

  72 Tage = ⁷²⁄₃₆₀Jahr = ³⁶⁄₁₈₀Jahr = ¹⁸⁄₉₀ Jahr = ⁹⁄₄₅Jahr = ⅕ Jahr.
• Teil 2: ⏳ Der zeitliche Faktor bei 1, 2, 3, ...Monaten

  Monatszinsen bestimmen aufgrund gegebener Jahreszinsen

  Zinsen bei einem, 2, 3, ... Monaten

  Sind die Jahreszinsen gegeben und die angelegte Zeitspanne des Geldes innerhalb eines Jahres, dann lässt sich das mit einem zeitlichen Faktor als Bruch ausdrücken und berechnen:
  Zinsen = Jahreszinsen · ^{zeitlicher Faktor}_{als Bruch}

  Beispiel 1: Jahreszinsen = 330 €, angelegte Zeit: ⅔ Jahr, zeitlicher Faktor ist der Bruch = ⅔
  Zinsen = 330 € ·  ² ₃ =¹¹⁰ 330 € ·  ² _3 1 = 220 €

  Beispiel 2: Jahreszinsen = 36 €, angelegte Zeit: 5 Monate und da ein Jahr 12 Monate hat ist der zeitliche Faktor =  ⁵ ₁₂
  Zinsen = 36 € ·  ⁵ ₁₂ =³ 36 € ·  ⁵ _12 1 = 15 €

  Monatszinsen geschickt berechnen

  Der Zinssatz sei p%=1,5 % =  ^1,5 ₁₀₀, das Kapital 4800€ und für 5 Monate bei der Bank angelegt. Wir multiplizieren die Zinsformel: Z = K · p% mit einem Bruch  ⁵ ₁₂, der den zeitlichen Anteil berücksichtigt:
  Zinsen = Kapital mal p% mal ^{Anzahl Monate}₁₂

  Jetzt geht es darum, geschickt zu Kürzen, das vereinfacht die Rechnung meist erheblich.

  So viel Geld gibt es von der Bank am Ende der angelegten Zeit: Dieses Geld kann man sich von der Bank tatsächlich auszahlen lassen.

  Hier gibt es Hilfen beim Kürzen, die entsprechenden Nullen sind durchgestrichen!

  Monatszinsen

  

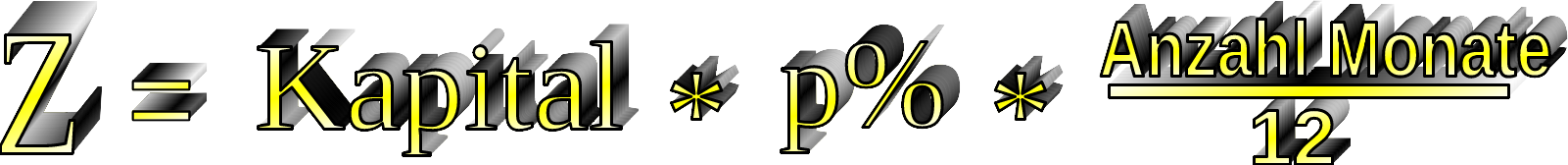
  Du hast nun den zweiten Teil, die Monatszinsen bearbeitet. Hervorragend!
  Atme wieder kurz durch, bevor der nächste Teil beginnt.

• Teil 3: Tageszinsen bei der 🏦 (Dort gilt: 1 Jahr hat 360 Tage)

  Tageszinsen bei der Bank

  Tageszinsen bei der Bank

  Tageszinsen geschickt berechnen

  Der Zinssatz sei p%=2 % =  ² ₁₀₀, das Kapital 18000€ und für 201 Tage bei der Bank angelegt. Wir multiplizieren die Zinsformel: Z = K · p% mit einem Bruch, der den zeitlichen Anteil berücksichtigt:
  Zinsen = Kapital mal p% mal ^{Anzahl Tage}₃₆₀

  Jetzt geht es darum, geschickt zu Kürzen, das vereinfacht die Rechnung meist erheblich.

  So viel Geld gibt es von der Bank am Ende der angelegten Zeit: Dieses Geld kann man sich von der Bank tatsächlich auszahlen lassen.

  ---

  Tageszinsen, Zinssätze von 1% bis 5%

  

  Du hast alles soweit bearbeitet? Prima, prima, prima!
  Mache einen Screenshot (mit der Punktzahl und deinem Namen) und schicke sie deinem Lehrer.