Mathematikela steht für: Mathematik mit elektronischen Arbeitsblättern

Wie möchtest du arbeiten?

Im Detektivmodus 🕵 kannst du Aufgaben ergründen 🔍 und es gibt auch Lösungstipps 💡.
Im Modus Hausaufgaben erhältst du am Ende einen Lösungssatz.
Im Prüfungsmodus ⏱ gibt es eine Zeitbegrenzung und du erhältst deine Punktzahl erst am Ende.

Aufträge

• Teil 1: Mit Geldbeträge rechnen

  Mit Geld rechnen

  
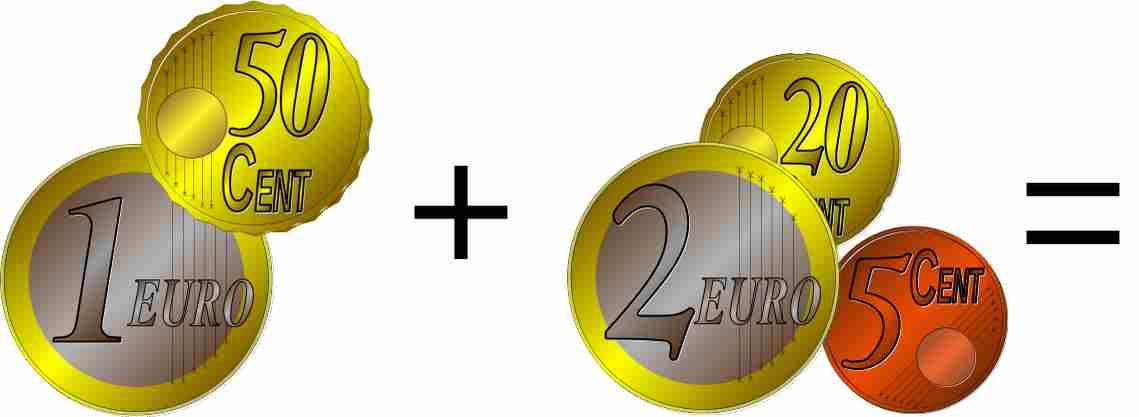
  Wie viel Euro ergibt das zusammen?

  Geldbeträge kann man addieren:

  Geldbeträge multiplizieren

  
  Wie viel Euro ergibt das multipliziert?

  Hast du es bemerkt? Der Faktor, mit dem wir multiplizieren ist eine pure Zahl. Dagegen ist der Geldbetrag in Euro angegeben.

  Die Angabe einer Geldmenge ist eine Größe

  

  Was ist eine Größe?

  Eine Größe ist stets zusammengesetzt aus einer Zahl und einer zugehörigen Einheit.

  Berechne, wenn du schneller sein möchtest, dann schreibe statt Euro die Kurzform der Einheit: €.

  In dieser Übung wurden Geldbeträge vervielfacht und das Ergebnis war wieder ein Geldbetrag.

  Das Vervielfachen einer Größe ergibt also wieder eine Größe, oder kurz:
  Zahl mal Größe ergibt Größe

  Alles gleiche Geldmengen:
  1,50 Euro = 1,50 € = 150 cent = 150 ct

  Eine Geldmenge im Euroraum kann man in Euro angeben, die Abkürzung für Euro ist €. Es gibt aber auch die Möglichkeit in Cent anzugeben. Dabei gilt, das 100 cent = 1 Euro sind.
  Beispiel: 2,22 € = 222 cent.
  Die Einheiten sind zwar verschieden, aber es ist die gleiche Geldmenge gemeint. Die Einheiten € und cent sind also von der gleichen Sorte. Nur daher können sie direkt umgerechnet werden.

  ½ mal 8 € = 0,5 mal 8 € = 4 €

  

  50 Prozent sind 0,5 und meint stets die Hälfte

  50% eines Geldbetrags meint stets die Hälfte davon.
  Gutes Gelingen.

  ⅒ mal 2 € meint den 10. Teil von 2 €

  ⅒ eines Geldbetrags ist stets der zehnte Teil davon.
  
  Volle Konzentration, es geht los!

  10% meint den 10. Teil

  10% eines Geldbetrags meint stets den zehnten Teil davon.
  
  Das kriegst du gut hin!
• Teil 2: Geld verteilen und Geld aufteilen

  Verteilen

  
  Verteilen meint, eine bestimmte Geldmenge wird z.B. an eine Anzahl Personen so verteilt, dass jeder die gleiche Menge bekommt

  Aufteilen

  
  Aufteilen meint, eine bestimmte Geldmenge wird in gleich große Teilbeträge gestückelt. Wie viele dieser Teilbeträge bekommt man dann?

  Aufteilen in Beträge wie 0,50€ oder 1,50 €

  
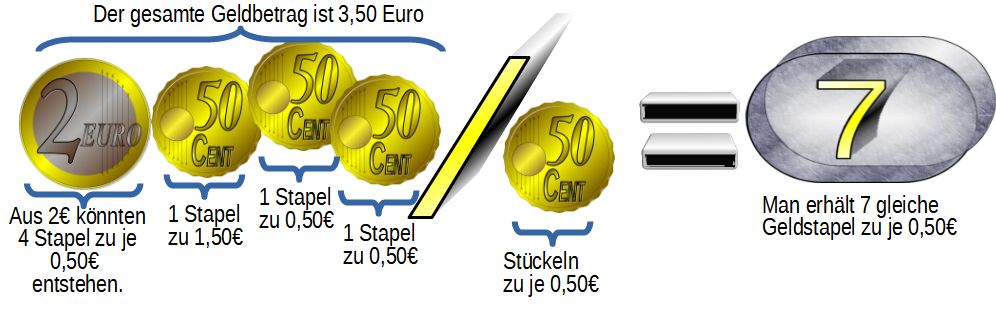
  Teilt man 1 € in 50cent Stücke auf, so braucht es davon genau 2.

  Aufteilen durch Beträge unter 1 €

  
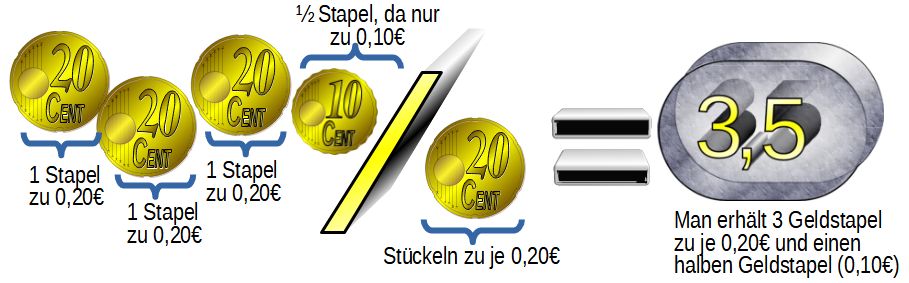
  Aufteilen bei Stückelungen, die unter 1 Euro sind, führen zu einer entsprechend großen Zahl an den Stückelungen.
• Teil 3: Geldmengen vermehren und Geldmengen vermindern

  Preise bzw. Geldmenge vermehren um das 1,1fache

  

  Im Alltag sagen wir häufig, der Preis einer Ware wird um 10 % (sprich: 10 Prozent)erhöht. Das Ergebnis entspricht genau diese Multiplikation mit 1,1!
  Denn: Der alte Preis entspricht 100% (😉 100% = 1) und die Erhöhung ist 10% (😉 10% = 0,1) .
  Somit sind: 100% + 10% = 1 + 0,1 = 1,1
  Eine Ware wird jeweils um 10% verteuert:

  Preise bzw. Geldmenge vermehren um das 1,5fache

  

  Im Alltag sagen wir häufig, der Preis einer Ware wird um 50 % erhöht. Das ist hier genau diese Multiplikation mit 1,5!
  Denn: Der alte Preis entspricht 100% (😉 100% = 1) und die Erhöhung ist 50% (😉50% = 0,5) .
  Somit sind: 100% + 50% = 1 + 0,5 = 1,5

  Preise bzw. Geldmenge vermehren um das 1,2fache

  

  Im Alltag sagen wir häufig, der Preis einer Ware wird um 20 % erhöht. Das ist hier genau diese Multiplikation mit 1,2!
  Denn: Der alte Preis entspricht 100% (😉 100% = 1) und die Erhöhung ist 20% (😉 20% = 0,2) .
  Somit sind: 100% + 20% = 1 + 0,2 = 1,2

  Preise bzw. Geldmenge vermehren um das 1,01fache

  

  Im Alltag sagen wir häufig, der Preis einer Ware wird um 1 % erhöht. Das ist hier genau diese Multiplikation mit 1,01!
  Denn: Der alte Preis entspricht 100% (😉 100% = 1) und die Erhöhung ist 1% (😉1% = 0,01) .
  Somit sind: 100% + 1% = 1 + 0,01 = 1,01

  Preise bzw. Geldmenge vermindern auf das 0,9fache

  

  Im Alltag sagen wir häufig, der Preis einer Ware wird um 10% vermindert. Das ist hier genau diese Multiplikation mit 0,9!
  Denn: Der alte Preis entspricht 100% (😉100% = 1) und die Minderung beträgt 10% (😉10% = 0,1).
  Somit sind: 100% - 10% = 1 - 0,1 = 0,9

  Preise bzw. Geldmenge vermindern auf das 0,8fache

  

  Im Alltag sagen wir häufig, der Preis einer Ware wird um 20% vermindert. Das ist hier genau diese Multiplikation mit 0,8!
  Warum ist das so?
  Der alte Preis entspricht 100% (😉100% = 1) und die Minderung beträgt 20% (😉20% = 0,2).
  Somit sind: 100% - 20% = 1 - 0,2 = 0,8

  Preise bzw. Geldmenge vermindern auf das 0,95fache

  

  Im Alltag sagen wir häufig, der Preis einer Ware wird um 5% reduziert wird. Das ist hier genau diese Multiplikation mit 0,95!
  Warum ist das so?
  Der alte Preis entspricht 100% (😉100% = 1) und die Minderung beträgt 5% (😉5% = 0,05).
  Somit sind: 100% - 5% = 1 - 0,05 = 0,95

  Preise bzw. Geldmenge vermindern auf das 0,98fache

  
  Oft gehen Preisnachlässe mit einer Verminderung um den Fünfzigsten Teil einher. Hier ein wichtiger Rechentipp, um den Fünfzigsten Teil zu bestimmen: Es ist das Doppelte vom Hundertsten Teil, da:
  ¹⁄₅₀ = ²⁄₁₀₀ = 2 mal ¹⁄₁₀₀ = 0,02
  Die Ware kostet dann das 0,98fache vom ursprünglichen Preis, denn: 1 - ²⁄₁₀₀ = 1 - 0,02 = 0,98
  Das Üben wir nun.

  Im Alltag sagen wir häufig, es gibt einen Rabatt um 2% (Rabatt bedeutet Preisnachlass). Das ist hier genau diese Multiplikation mit 0,98!
  Warum ist das so?
  Der alte Preis entspricht 100% (😉100% = 1) und die Minderung beträgt 2% (😉2% = 0,02).
  Somit sind: 100% - 2% = 1 - 0,02 = 0,98

  Herzliche Glückwünsche, du hast es weit gebracht...

  😁 Merkst du, wie deine Kenntnisse in Mathematik besser werden? 😉