Mathematikela steht für: Mathematik mit elektronischen Arbeitsblättern

Wie möchtest du arbeiten?

Im Detektivmodus 🕵 kannst du Aufgaben ergründen 🔍 und es gibt auch Lösungstipps 💡.
Im Modus Hausaufgaben erhältst du am Ende einen Lösungssatz.
Im Prüfungsmodus ⏱ gibt es eine Zeitbegrenzung und du erhältst deine Punktzahl erst am Ende.

Aufträge

• Teil 1: Zahl mal eine Größe, also eine Größe vervielfachen

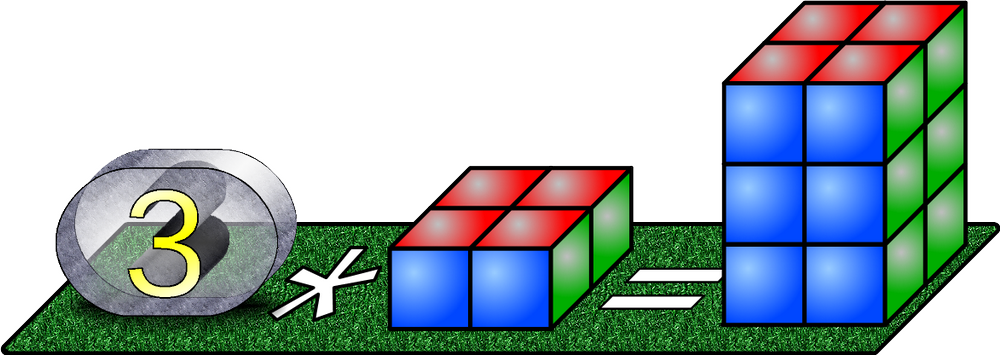
  Wie viele Würfel sind es jeweils?

  Diese Würfel stehen nicht nur für eine Zahl, es ist eine bestimmte Menge an Würfeln. In der Naturwissenschaft nennen wir das dann eine Größe. Eine Größe hat immer zuerst eine Zahl, dann folgt die Einheit.

  Eine Größe mit einer Zahl multiplizieren

  

  Die Angabe einer Geldmenge ist auch eine Größe

  

  Was ist jetzt eine Größe?

  Eine Größe ist stets zusammengesetzt aus einer Zahl und einer zugehörigen Einheit.

  Berechne, wenn du schneller sein möchtest, dann schreibe statt Euro die Kurzform der Einheit: €.

  In dieser Übung wurden Geldbeträge vervielfacht und das Ergebnis war wieder ein Geldbetrag.

  Das Vervielfachen einer Größe ergibt also wieder eine Größe, oder kurz:
  Zahl mal Größe ergibt Größe

  Geldbeträge multiplizieren

  
  Wie viel Euro ergibt das multipliziert?

  Hast du es bemerkt? Der Faktor, mit dem wir multiplizieren ist eine pure Zahl. Dagegen ist der Geldbetrag in Euro angegeben.

  Die Hälfte, ein Drittel, ein Viertel, ... von einer Größe
  Oder: Wie viel ist ½ mal die Größe?

  
  

  Einen Bruch mit einer Größe multiplizieren

  

  
  Tipp: Der Bruch ⅔ ist wie: 2 mal ⅓ (also ⅓ berechnen, dann noch verdoppeln)
  
  

  Der Bruch ⅖

  
  Tipp: Der Bruch ⅖ ist wie 2 * ⅕ (also das doppelte von ⅕)
  

  Der Bruch ⅚

  
  Tipp: Der Bruch ⅚ ist wie 5 * ⅙ (also das Fünffache von ⅙)
  

  Weitere Übungen

  

  Weitere Übungen und dazu ein Rechentipp:
  Für ⁵ ₁₂rechne durch drei, dann durch 4 und dann mal 5.
  

  Für ⁷ ₁₅rechne erst den Geldbetrag durch 5, dann durch 3, multipliziere mit 7
  
  

  Für ³ ₂₀rechne den Geldbetrag durch 10, halbiere nochmals, multipliziere mit 3
  
  

  Für ¹¹ ₁₈rechne durch 6, dann nochmals durch 3, multipliziere mit 11
  
  

  Für ² ₂₁rechne durch 7, dann durch 3, verdopple dann
  
  

  Für ⁵ ₂₄rechne durch 8, dann durch 3 und verfünffache nun
  
  

  Für ¹¹ ₃₀rechne durch 10, dann durch 3 und dann mal 11
  
  

  Für ⁷ ₅₀rechne durch 100, verdopple anschließend, und nimm noch mal 7.

  Größen addieren

  
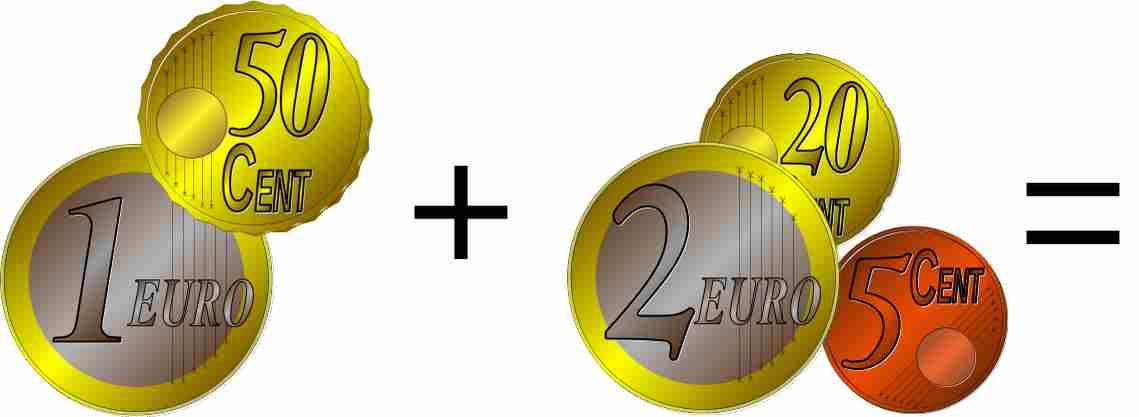
  Wie viel Euro ergibt das zusammen?

  Größen mit gleichen Einheiten kann man addieren oder subtrahieren. Das Ergebnis ist wieder eine Größe.

  Ein Drittel mal eine Größe mal ein Fünftel
  Oder: Wie viel ist ⅓ mal Geldbetrag mal ⅕?

  
  

  Zwei Drittel mal eine Größe mal zwei Fünftel
  Oder: Wie viel ist ⅔ mal Geldbetrag mal ⅖?

  
  

  Du hast nun diesen Teil bearbeitet. Hervorragend!
  Atme mal durch.

• Teil 2: Von der Kunst, Größen zu wandeln

  Umwandeln von einer Größe in eine Größe mit anderer Einheit

  Die Ausgangsgröße aus dem 1. Bereich hat die Einheit: Würfel
  Jeder Würfel kostet einen bestimmten Betrag. Es gibt einen 'Umwandlungsfaktor'. Dieser hat einen Wert, hier 5 und im Anschluss die zusammengesetzten Größe:    ^€   _Würfel
  

  1. Größe mal Umwandlungsfaktor =Zielgröße

  1. Größe: Die Menge der Würfel
  Umwandlungsfaktor, er hat zwei Einheiten:     ^€   _Würfel
  Der Einheit im Nenner (Würfel) sorgt dafür, dass die Einheit der 1. Größe aufgehoben wird.
  Zielgröße: Diese ist der zu zahlende Betrag in der Einheit €.

  Weitere Übungen:

  So viel Stunden hat jemand gearbeitet. Er verlangt einen bestimmten Preis pro Stunde (pro h), was ist zu zahlen?

  Die Größe aus dem 1. Bereich enthält die Angabe, wie viele Stunden gearbeitet wurden.
  Der Arbeitspreis gibt an, was eine Stunde kostet (in Euro pro Stunde, kurz: €/h)
  Beides multipliziert ergibt den Betrag, der zu zahlen ist.

  In kleinere oder größere Flächeneinheiten umwandeln

  Die Größe aus dem 1. Bereich ist ein Flächeninhalt und soll in eine feinere Flächeneinheit gewandelt werden.
  Beobachte genau: Legst du 10 quadratische Stücke mit 1cm² nebeneinander, so erhältst du eine Reihe mit 10cm². Legst du nun 10 dieser Reihen übereinander, dann erhältst du 100cm² und diese füllen genau 1 dm².
  Es gilt also:
  1 dm² = 100 cm² Die Umwandlungszahl bei Flächen ist damit 100.

  Jetzt werden wir von der kleineren Flächeneinheit (dm²) auf die nächstgrößere Flächeneinheit (dm²) wandeln:
  

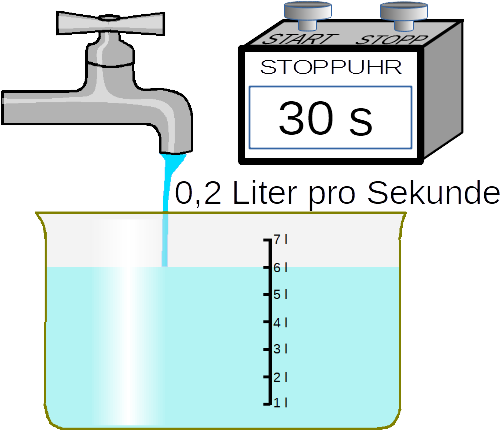
  Wie lange dauert das Füllen, Wasserströme berechnen

  Die 1. Größe ist eine Zeitspanne, außerdem ist die Wasserstromstärke gegeben. Die 2. Größe ergibt dann die Wassermenge
  

  Wie viel Weg legt der Fahrradfahrer zurück?

  Die 1. Größe ist wieder eine Zeitspanne, außerdem ist die Geschwindigkeit (als Umwandlungsfaktor) angegeben. Als Ergebnis erhält man die zurückgelegte Wegstrecke
  Die Geschwindigkeit hat die zusammengesetzte Einheit: Meter pro Sekunde. Die Angabe 7 Meter pro Sekunde heißt, dass der Fahrradfahrer in jeder Sekunde 7 Meter zurücklegt.
  Die Geschwindigkeit hat das Formelzeichen v und wir schreiben die Einheit Meter pro Sekunde kürzer: ^m⁄_s