Mathematikela steht für: Mathematik mit elektronischen Arbeitsblättern
Wie möchtest du arbeiten?
🕵🖋
⏱
Im Detektivmodus 🕵 kannst du Aufgaben ergründen 🔍 und
es gibt auch Lösungstipps 💡.
Im Modus Hausaufgaben erhältst du am Ende einen Lösungssatz.
Im Prüfungsmodus ⏱ gibt es eine Zeitbegrenzung und du erhältst deine Punktzahl erst am Ende.
Aufträge
-
Teil 1: Idee, wie Gleichungen gelöst werden
Erste Gleichungen lösen
Beispiel für das Lösen einer Gleichung:
x + 8 = 10 Sprich es so aus: "x plus 8 gleich 10"
-8 ↓ ↓ -8
x = 2 Sprich es so aus: "x gleich 2"
Also gilt für die Gleichung x+8 = 10, dass die Unbekannte x den Wert 2 haben muss.Beim Gleichungen lösen gibt es folgendes Ziel:
Ist x auf einer Seite allein, das ist fein.
Auf der anderen Seite der Gleichung steht dann die gesuchte Zahl. An jeder Stelle der Gleichungen kann man sich nun statt x diese gesuchte Zahl denken.Beispiel für das Lösen einer Gleichung mit x:
x + 25 = 30 Sprich es so aus: "x plus 25 gleich 30"
-25 ↓ ↓ -25
x = 5 Sprich es so aus: "x gleich 5"Statt:
x + 25 = 30
kann man sich nun auch denken:
5 + 25 = 30
Das ist gleichzeitig auch die 'Probe', die linke und rechte Seite der Gleichung ergeben hier den gleichen Wert, es ist jeweils 30.
Diese Waage ist im Gleichgewicht! Links ist
x+2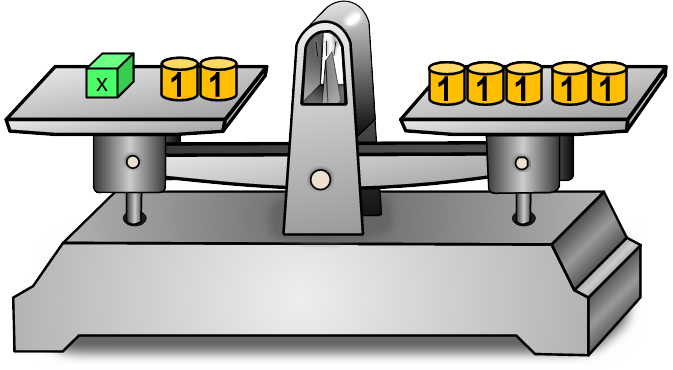
Das unbekannte Gewicht x kennen wir (noch) nicht.Rechts ist 5.
linke Seite 👇 ⚖ 👇 rechte Seite = -2 ↓ ↓ -2 x =
Antwort: Das Gewicht von x beträgt also .
Was ist die Idee beim Lösen von Gleichungen?Wir formen eine Gleichung Schritt für Schritt um und am Ende steht x allein auf einer Seite. Dann steht auf der anderen Seite die gesuchte Zahl. Jeden neuen Schritt schreiben wir in einer neuen Zeile und Änderungen erfolgen nach bestimmten Regeln. Übersetzt auf die Balkenwaage ⚖:
Eine Änderung ist erlaubt, wenn die Waage im Gleichgewicht bleibt.
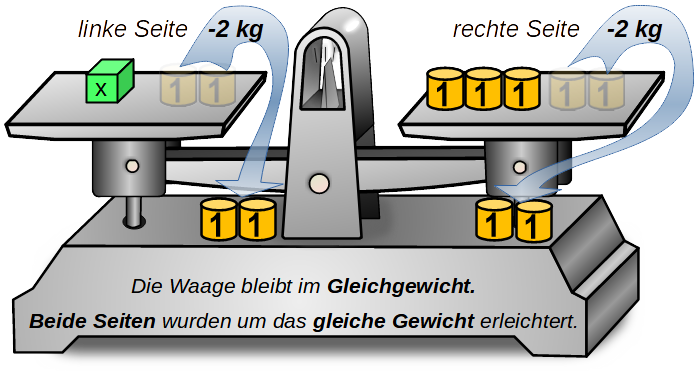 Auf der Balkenwaage würden man auf beiden Seiten 2 kg entfernen, dann ist x allein auf einer Seite.
Auf der Balkenwaage würden man auf beiden Seiten 2 kg entfernen, dann ist x allein auf einer Seite.
Löse diese Gleichungen mit der Unbekannten x
linke Seite 👇 ⚖ 👇 rechte Seite x + 8 = 12 -8 ↓ ↓ -8 x = Was muss der Wert von x sein? Überlege 🤔💭 kurz, du kommst bestimmt dahinter. 👆
Bestimme den Wert von x
linke Seite 👇 ⚖ 👇 rechte Seite x + 12 = 20 -12 ↓ ↓ -12 x =
Bestimme den Wert von x
linke Seite 👇 ⚖ 👇 rechte Seite x + 50 = 70 -50 ↓ ↓ -50 x =
Bestimme den Wert von x
linke Seite 👇 ⚖ 👇 rechte Seite x + 5 = 12 + 8 ↓ ↓ rechte Seite vereinfachen x + 5 = -5 ↓ ↓ -5 x =
Bestimme den Wert von x
linke Seite 👇 ⚖ 👇 rechte Seite x + 9 = 20·4 ↓ ↓ rechte Seite vereinfachen x + 9 = -9 ↓ ↓ -9 x =
Bestimme den Wert von x
linke Seite 👇 ⚖ 👇 rechte Seite x + 4 = 35 : 5 ↓ ↓ rechte Seite vereinfachen x + 4 = -4 ↓ ↓ -4 x =
Gleichungen nach x auflösen:
Wichtig ist dabei der weltweite 🗺️ StandardWas ist das Ziel beim Lösen einer Gleichung?
Antwort: x allein ist fein.
Am Ende der Umformungen steht zum Beispiel: x = 22Bei dem weltweiten Standard 🗺️ lösen wir Gleichungen mit der Unbekannten x:
- Schritt für Schritt.
Dabei werden die Gleichheitszeichen = der Gleichung stets untereinander geschrieben. - Änderungen, die beide Seiten der Gleichung betreffen werden mit einem senkrechten Strich | angekündigt. Wir nennen diesen senkrechten Strich gerne 'Kommandostrich' und hinter dem | folgt eine Aktion, die dann unbedingt beidseitig durchgeführt wird.
Diese Art der beidseitigen Umformungen ändern die Lösung für x nicht. - Das Ziel aller Umformungen der Gleichung: x allein ist fein. Wir sind fertig, wenn da nur noch steht: x = Zahlwert
Beispiel:
x+8 = 12 |-8 Wir subtrahieren -8 auf beiden Seiten, damit x alleine steht
x = 12-8
x = 4
Noch ein Hinweis: Jede Zeile einer Gleichung schreiben wir so, dass das Gleichheitszeichen = stets gleich eingerückt steht.Diese Waage ist im Gleichgewicht. Das was links und rechts auf ihr liegt kann als Gleichung notiert werden. 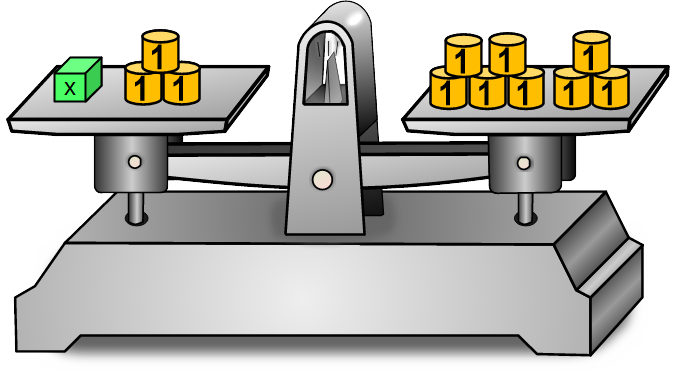
Notiere die linke Seite hier 👇 ⚖️ Hier 👇 die rechte Seite notieren = | Welche Strategie darf man nun anwenden, um die Gleichung zu lösen? 1. Lösungsstrategie: Die Gleichung bleibt im Gleichgewicht, wenn man die gleiche Menge auf jeder Seite wegnimmt. 👆 Diese beidseitige 'Aktion' geben wir ganz rechts mit einem senkrechten Strich an, hier ist es: |-3 x =
Das was auf der Waage liegt kann als Gleichung geschrieben werden. 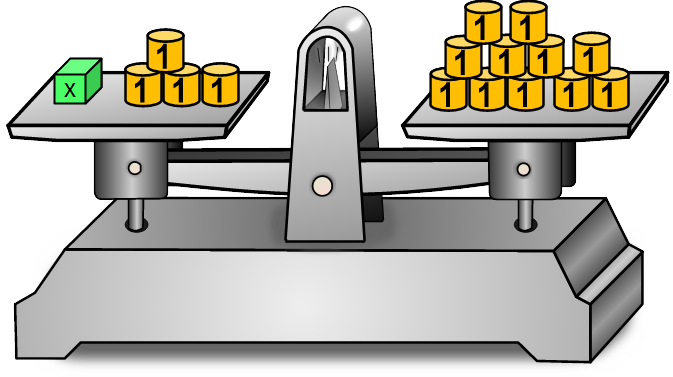
linke Seite ⚖️ rechte Seite | Aktion = | x =
Löse die Gleichung x+40=65 nach dem weltweiten Standard
linke Seite ⚖️ rechte Seite | Aktion x+40 = 65 | x =
Löse die Gleichung x+2,5=6 nach dem weltweiten Standard
linke Seite ⚖️ rechte Seite | Aktion x+2,5 = 6 | x =
Gleichungen lösen: 🎈🎈🎈 Heliumballons ziehen nach oben!
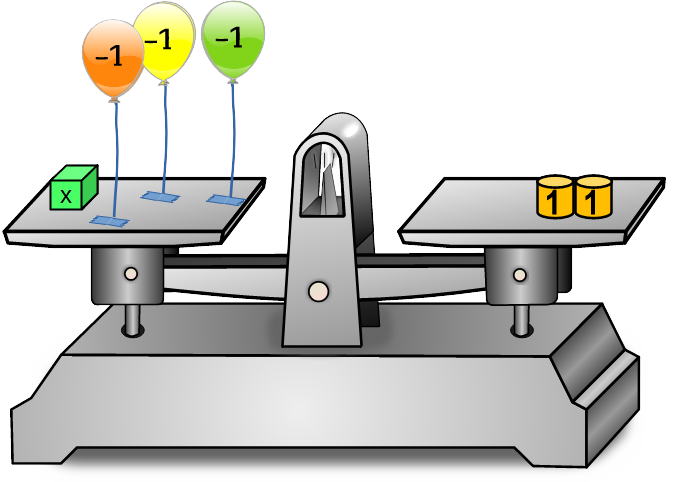
= | x-3+ = 2+ x = Welche Strategie darf man hier anwenden, um die Gleichung zu lösen?
2. Lösungsstrategie: Die Gleichung bleibt im Gleichgewicht, wenn man die gleiche Menge auf jeder Seite hinlegt.👆 Diese beidseitige 'Aktion' geben wir ganz rechts mit einem senkrechten Strich an, hier ist es: |+3 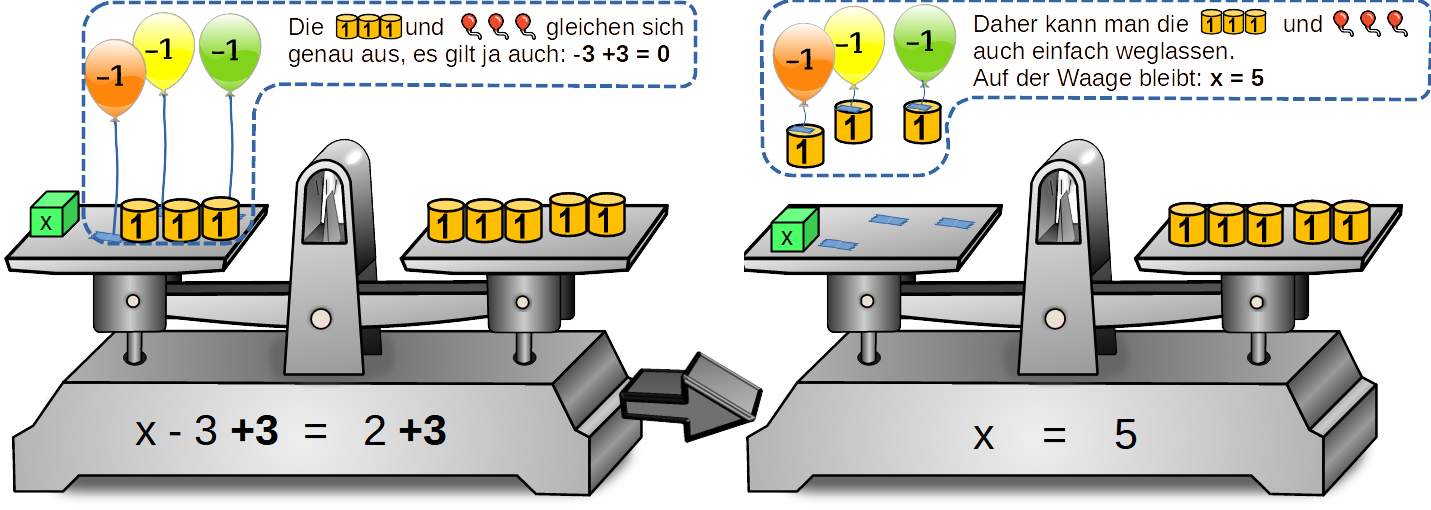
Und jetzt ziehen 🎈🎈🎈🎈🎈 Heliumballons eine Seite nach oben
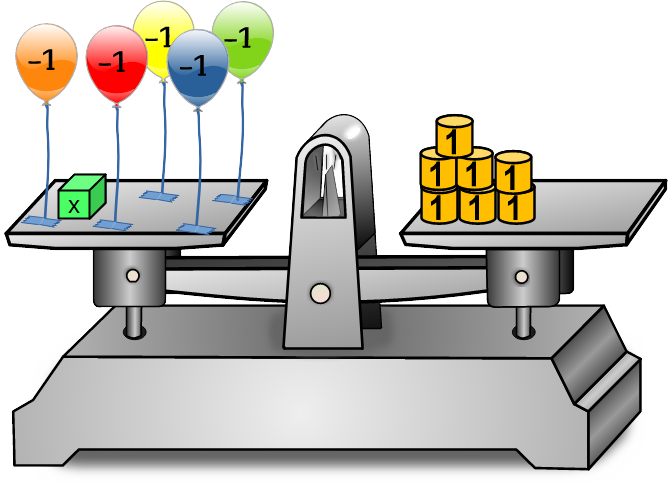
linke Seite ⚖️ rechte Seite | Aktion = | x = Eine weitere Übung
Löse die Gleichung nach der Unbekannten x auf
linke Seite ⚖️ rechte Seite | Aktion x-33 = 44 | x = Weitere Übungen
Löse die Gleichung nach der Unbekannten x auf
linke Seite ⚖️ rechte Seite | Aktion x+4+5 = 30-15 | Vereinfache = | x = Löse die Gleichung nach der Unbekannten x auf
linke Seite ⚖️ rechte Seite | Aktion x+5-7 = 4·5 | Vereinfache = | x = Löse die Gleichung nach der Unbekannten x auf
linke Seite ⚖️ rechte Seite | Aktion 8+x+12-30 = 7·4 + 2 | Vereinfache = | x = Löse die Gleichung nach der Unbekannten x auf
linke Seite ⚖️ rechte Seite | Aktion x-30,5 = -10,5 | x = Mehrere x auf einer Seite, zum Beispiel x+x+x
Wie lautet die Gleichung 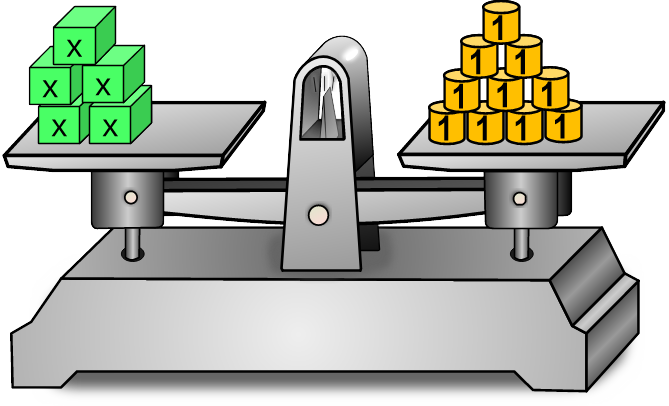
linke Seite ⚖️ rechte Seite |Änderungen links und rechts x+x+x+x+x = Wir fassen da 👇 die x+x+x+x+x zu 5x zusammen. = | Welche Strategie darf man nun anwenden, um die Gleichung zu lösen? 3. Lösungsstrategie: Die Gleichung bleibt im Gleichgewicht, wenn man beide Seiten durch die gleiche Zahl teilt. 👆 Diese beidseitige 'Aktion' geben wir ganz rechts mit einem senkrechten Strich an, hier ist es: |:5 x =
Weitere Übungen
linke Seite 👇 ⚖ 👇 rechte Seite 4x = 12 :4 ↓ ↓ :4 x =
linke Seite 👇 ⚖ 👇 rechte Seite 6x = 48 :6 ↓ ↓ :6 x =
linke Seite 👇 ⚖ 👇 rechte Seite 15x = 30 :15 ↓ ↓ :15 x =
Mehrere x auf einer Seite, dazu eine Zahl
Die Waage ist im Gleichgewicht! 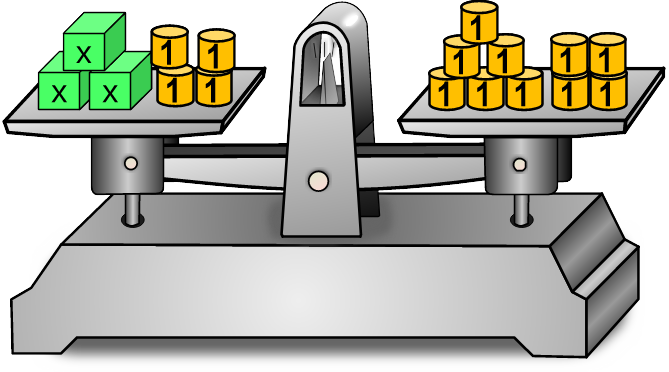
Links ist x+x+x + 4 und rechts ist 10.
Das unbekannte Gewicht x kommt hier nun dreimal vor, also: x+x+x und dazu kommt noch 4.linke Seite 👇
=👇 rechte Seite |👇 Aktionen
|= | Wir wissen nun: 3x sind gleich 6 👆. Wir wollen aber wissen, wie viel nur ein x ist. Daher dividieren wir als Aktion durch die Zahl 3. |👆 Hier nun durch drei dividieren x = Mehrere x auf einer Seite
Die Waage ist im Gleichgewicht! 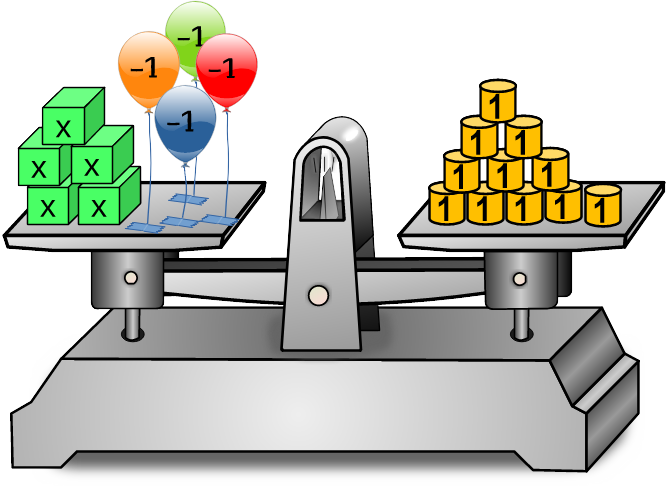
links 👇
=👇 rechts |👇 Aktionen
|= | x = Mehrere x vermindert um eine Zahl
Die Waage ist im Gleichgewicht! 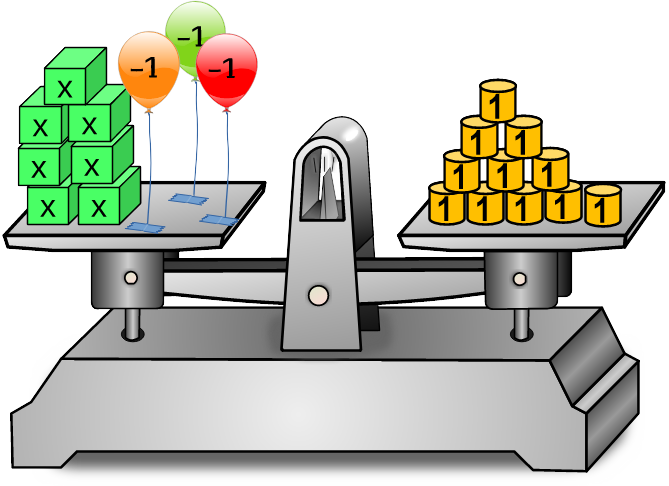
links 👇 = 👇rechts | Aktionen = | = | x = - Schritt für Schritt.
-
Teil 2: Gleichungen lösen
Gleichungen lösen, x ist nur auf einer Seite
Vereinfache zuerst beide Seiten
(Rechentipp: x+x+x+x = 4x)linke Seite ⚖️ rechte Seite | Änderungen links und rechts x+x+x+x = 20 = |: x = Gleichung lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinBei jedem Schritt bleibt die Gleichung im Gleichgewicht ⚖️. linke Seite ⚖️ rechte Seite | Änderungen links und rechts x+2x+30 = 51 | zuerst vereinfachen = 51 | = |: x = Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinBei jedem Schritt bleibt die Gleichung im Gleichgewicht ⚖️. linke Seite ⚖️ rechte Seite | Änderungen links und rechts 2x+3x-10-10 = 25 | zuerst vereinfachen = 25 | + = |: x = Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinBei jedem Schritt bleibt die Gleichung im Gleichgewicht ⚖️. linke Seite ⚖️ rechte Seite | Änderungen links und rechts 9x-3x+10-40 = 12 | zuerst vereinfachen = 12 | + = | : x =
Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinBei jedem Schritt bleibt die Gleichung im Gleichgewicht ⚖️. linke Seite ⚖️ rechte Seite | Änderungen links und rechts 4x-3x+7x-22 = 9·2+24 | zunächst vereinfachen = | + = | : x = Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinBei jedem Schritt bleibt die Gleichung im Gleichgewicht ⚖️. linke Seite ⚖️ rechte Seite | Änderungen links und rechts 6x-4x+7x+8 = 6·4+20 | zunächst vereinfachen = | = | x = Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinlinke Seite ⚖️ rechte Seite | Änderungen links und rechts 14x-6x-7·2 = 6·5-12 | zunächst vereinfachen = | = | x = Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinlinke Seite ⚖️ rechte Seite | Änderungen links und rechts 44x+7-33x = 10-25 | zunächst vereinfachen = | = | x =
Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinlinke Seite ⚖️ rechte Seite | Änderungen links und rechts 9+33x-15-30x = 20-10·5 | zunächst vereinfachen = | = | x =
Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinlinke Seite ⚖️ rechte Seite | Änderungen links und rechts 10x-12x+15 = 5·5-4 | zunächst vereinfachen = | = | x =
Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinlinke Seite ⚖️ rechte Seite | Änderungen links und rechts 23x+8-30x-20 = 7·6-3·4 | zunächst vereinfachen = | = | x =
Gleichungen lösen
Mit jeder neuen Zeile nähern wir uns diesem Ziel: x allein ist feinlinke Seite ⚖️ rechte Seite | Änderungen links und rechts 12x-10x+20-11x+10 = 15-30 | zunächst vereinfachen = | =️ | x =
Du hast nun diesen Teil bearbeitet. Hervorragend!
Atme mal durch.
Diese Übungen mit dem Zinseszinseffekt waren erst der Anfang. Es ist wichtig, dass du das auch auf Papier bearbeitest, um ein eigenes Erlebnis davon zu bekommen. -
Teil 3: Gleichungen der Form 8x + 15 = 4x + 8
Gleichungen lösen, x ist auf beiden Seiten
Mehrere x sind auf der linken und auf der rechten Seite
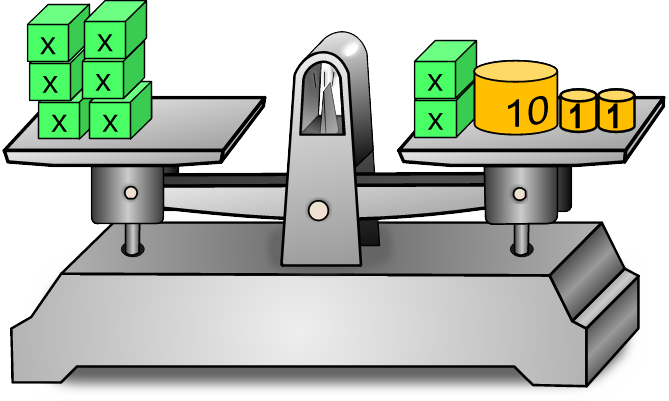
Tipp: Entferne auf beiden Seiten jeweils 2x, dann stehen die x nur noch auf einer Seite.links 👇 = 👇 rechts | Aktionen = | = | x =
Löse eine weitere Gleichung
Tipp: Entferne auf beiden Seiten jeweils 6x, dann steht die Unbekannte x nur noch auf einer Seite.
links 👇 = 👇 rechts | Aktionen 10x = 6x + 32 | = | x = Die Unbekannte x ist auf beiden Seiten der Gleichung
Löse diese Gleichung nach x auf
links 👇 = 👇 rechts | Aktionen 20x = 14x + 24 | = | x =
Löse diese Gleichung nach x auf
links 👇 = 👇 rechts | Aktionen 14,5x = 2,5x + 24 | = | x =
Löse die Gleichung nach x auf
links 👇 = 👇 rechts | Aktionen 33x = 13x + 10 | = | x = Die Unbekannte x ist auf der linken und auf der rechten Seite
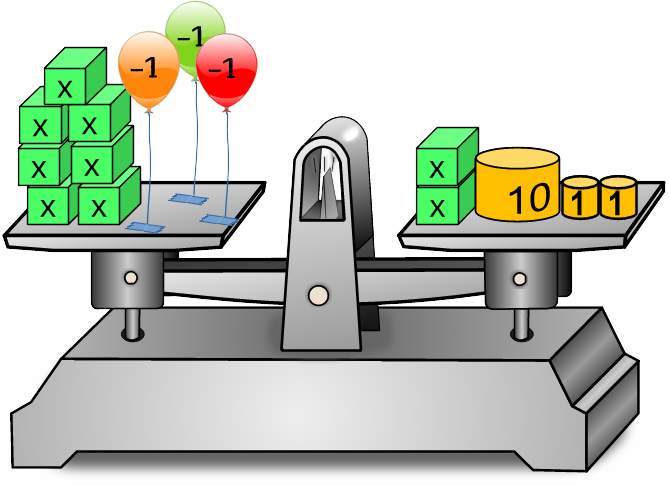
Tipp: Entferne zuerst auf beiden Seiten jeweils 2x, dann stehen die x nur noch auf einer Seite.links 👇 = 👇 rechts | Aktionen = | -2x = | = | x =
Löse diese Gleichung nach x auf
Mehrere x sind auf der linken und auf der rechten Seite
Tipp: Entferne zuerst auf beiden Seiten 18x, dann steht die Unbekannte x nur noch auf einer Seite.links 👇 = 👇 rechts | Aktionen 25x = 18x - 21 | = | x = -
Teil 4: Erste Textaufgaben
Textaufgaben mit Gleichungen
Ich denke mir eine Zahl. Wenn ich diese Zahl um 25 erhöhe und anschließend 14 abziehe, so erhalte ich 60
Tipp: Wir sagen, die gesuchte Zahl sei x.
links 👇 = 👇 rechts | Aktionen = | Vereinfache
| die linke Seite= | x = Damit ist die gesuchte Zahl .
Ich denke mir eine Zahl. Wenn ich diese Zahl verdreifache und anschließend 20 abziehe, so erhalte ich 70
Tipp: Wir sagen, die gesuchte Zahl sei x.
links 👇 = 👇 rechts | Aktionen = | = | x = Damit ist die gesuchte Zahl .
Summe = Addieren, Differenz bedeutet subtrahieren und Produkt bedeutet Multiplizieren
Die Summe einer Zahl und 27 ergibt 30.
Tipp: "Eine(r) Zahl" ist unsere gesuchte Zahl, das ist unser x.
links 👇 = 👇 rechts | Aktionen = | x = Damit ist die gesuchte Zahl .
Die Differenz einer Zahl x mit 40 ergibt 80.
Tipp: "Eine(r) Zahl" ist unsere gesuchte Zahl, das ist unser x.
links 👇 = 👇 rechts | Aktionen = | x = Damit ist die gesuchte Zahl .
Das Produkt einer Zahl mit 10 ergibt ergibt 330.
Tipp: "Eine(r) Zahl" ist unsere gesuchte Zahl, das ist unser x.
links 👇 = 👇 rechts | Aktionen = | x = Damit ist die gesuchte Zahl . - Teil 5: Wie alt ist eigentlich ...
Gleichungen mit x lösen, um das Alter einer Person zu bestimmen
👨👧 Vater und Tochter: Der Vater ist 4-mal so alt wie die Tochter. Zusammen sind sie 45 Jahre alt.
Tipp: Wir sagen, das Alter der Tochter sei x.
👧 Alter der Tochter: 👨Alter des Vaters: Zusammen sind sie so viele Jahre alt: Nun werden obige Angaben in eine Gleichung übersetzt:
Alter der Tochter + Alter des Vaters = 45links 👇 = 👇 rechts | Aktionen = | Vereinfache
| die linke Seite= | x = Damit ist die Tochter Jahre alt (👧=x). Damit ist der Vater dann Jahre alt (👨=4x).
Gleichungen mit x lösen, um das Alter einer Person zu bestimmen
👩👧👦Mutter, Tochter und Sohn: Die Mutter ist ist 7-mal so alt wie ihr Sohn Max. Ihre Tochter Nele ist doppelt so alt wie Max. Zusammen sind sie 60 Jahre alt.
Tipp: Wir sagen, das Alter von Max sei x.
👦 Alter von Max: 👧 Alter von Nele: 👩 Alter der Mutter: Zusammen sind sie so viele Jahre alt: Nun werden obige Angaben in eine Gleichung übersetzt:
Alter von Max 👦 + Alter von Nele 👧 + Alter der Mutter 👩 = 60links 👇 = 👇 rechts | Aktionen = | Vereinfache
| die linke Seite= | x = Damit ist Max Jahre alt (👦=x). Damit ist Nele Jahre alt (👧=2x). Damit ist die Mutter dann Jahre alt (👩=7x).
Wie alt sind die Freundinnen?
Ines, Lara und Berivan sind zusammen 38 Jahre alt.
Dabei ist Ines doppelt so alt wie Lara.
Berivan ist 2 Jahre älter als Lara.Tipp: Wir sagen, das Alter von Lara sei x.
👩 Alter von Lara: 👧 Alter von Ines: 🙋 Alter von Berivan: Zusammen sind sie so viele Jahre alt: Nun werden obige Angaben in eine Gleichung übersetzt:
👩 Alter von Lara + Alter von Ines 👧 + Alter von Berivan 🙋 = 38links 👇 = 👇 rechts | Aktionen = | Vereinfache
| die linke Seite= | = | x = Damit ist Lara Jahre alt (👩=x). Damit ist Ines Jahre alt (👧=2x). Damit ist Berivan Jahre alt (🙋=x+2).
Einen Lottogewinn teilen
3 Brüder teilen einen Lottogewinn über 6500 €.
Der Jüngste erhält 500 € weniger als der Mittlere.
Der Älteste erhält 1000 € mehr als der Mittlere. Aber wie viel Geld kriegt nun jeder von ihnen?Tipp: Wir sagen, der Mittlere erhalte x.
Der Mittlere erhalte: Der Jüngste erhält dann: Der Älteste erhält dann: Zusammen erhalten sie: Nun werden obige Angaben in eine Gleichung übersetzt.
links 👇 = 👇 rechts | Aktionen = | Vereinfache
| die linke Seite= | = | x = Damit erhält der Jüngste . (Der Jüngster erhält x-500) Damit erhält der Mittlere . (Der Mittlere erhält x) Damit erhält der Älteste . (Der Älteste erhält x+1000)
- Teil 6: Gleichungen lösen mit Figuren
Gleichungen mit Figuren x lösen
Der Umfang dieses Rechtecks beträgt 36 cm. Wie lang sind die Seiten?
Tipp: Wir sagen, die Länge sei3x.

Der Umfang des Rechtecks beträgt 36 cm.Lange Seite des Rechtes (Länge) kurze Seite des Rechtecks (Breite) Umfang des Rechtecks: Nun werden obige Angaben in eine Gleichung übersetzt:
obere Seite + untere Seite + linke Seite + rechte Seite= 36links 👇 = 👇 rechts | Aktionen = | Vereinfache
| die linke Seite= | x = Damit ist die Länge des Rechtecks: cm. Damit ist die Breite des Rechtecks cm.
- Teil 7: 📦 Auspacken von Termen mit Klammern 📦
Ein Klammerausdruck wie (2x+5) ist wie ein 📦 Paket:
( ) Klammern und 📦 Pakete halten etwas zusammen- Teil 8: Gleichungen mit Klammern
Klammern ( ) halten etwas zusammen, so wie ein Paket 📦.
Auch Gleichungen können einen Ausdruck mit Klammern enthalten. Um diese Gleichungen zu lösen müssen die Klammern aufgelöst werden
Hinweis: Die Klammern haben kein Gewicht.
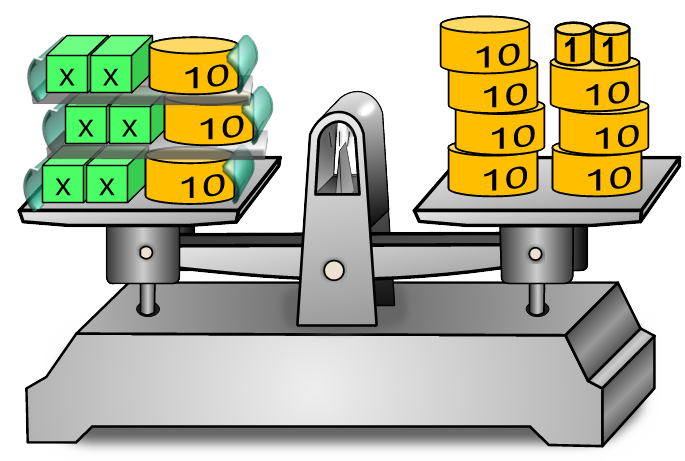
Auf der linken Seite ist IN KLAMMERN dreimal der gleiche Ausdruck.
Was steht in jeder Klammer? Wie oft kommt die Klammer vor? Dreimal kommt das Paket (2x+10) vor und wir schreiben folgenden Ausdruck kurz mit nur einer Klammer: links 👇 = 👇 rechts | Aktionen = | Die Klammer
| auflösen= | = | x = Jede Klammer (2x+10) hat damit einen Wert von
Löse nun dies: 7(3x+5) = 100-2
links 👇 = 👇 rechts | Aktionen 7 (3x + 5) = 100-2 | Klammer
| auflösen= | = | x = Jede Klammer (3x+5) hat damit einen Wert von
Eine weitere Aufgabe: 10(0,3x+0,5) = 75-10
links 👇 = 👇 rechts | Aktionen 10(0,3x+0,5) = 75-10 | Die Klammer
| auflösen= | = | x = Jede Klammer (0,3x + 0,5) hat damit einen Wert von
Und noch eine Aufgabe: 5(6x-4) = 40:4
links 👇 = 👇 rechts | Aktionen 5(6x-4) = 40:4 | Die Klammer
| auflösen= | = | x = Jede Klammer (6x-4) hat damit einen Wert von
Noch ein Beispiel 4(2x-12) = 8·3
links 👇 = 👇 rechts | Aktionen 4(2x-12) = 8·3 | Die Klammer
| auflösen= | = | x = Jede Klammer (2x-12) hat damit einen Wert von
Noch ein Beispiel 5·11+5(3x-7) = 20·4
links 👇 = 👇 rechts | Aktionen 5·11+5(3x-7) = 20·4 | Die Klammer
| auflösen= | Vereinfache
| links= | = | x = Jede Klammer (3x-7) hat damit einen Wert von
Impressum Idee und Umsetzung: J.Kreutzer - Teil 5: Wie alt ist eigentlich ...